一問一答の一歩

隣り合う辺の比が正解です

三角形において内角の二等分線は対応する辺を分割する比率については、証明に関しては補助線を用いた相似を用いるのですが、割と分かりやすいので、覚えてしまっても問題ないように思えます。

チェバの定理が正解です

チェバの定理は、三角形において長さの比を出すために使用する定理です。
下記のチェバの定理の式だけを見ると、どこに何を適応すれば良いか分かりにくく、複雑そうですが、対応する辺を一周するように当てはめると理解すると、公式の当てはめ方は定着しやすいです。

• (左上)(左下)×(底辺左)(底辺右) ×(右下)(右上) =1

※本ページでは(左上)から反時計回りで記載したが、一周の順番になっていればどこから始めても時計回りでも分子と分母が逆でもいい。

また、チェバの定理はメネラウスの定理と非常によく似ているのですが、メネラウスの定理は「ブ－メラン形」のときに長さの比を導出するのに使用されます。

メネラウスの定理が正解です

メネラウスの定理は、ブ－メラン形の図形において長さの比を出すために使用する定理です。

下記のメネラウスの定理の式だけを見ると、どこに何を適応すれば良いか分かりにくく、複雑そうですが、対応する辺を一周するように当てはめると理解すると、公式の当てはめ方は定着しやすいです。

• (左上)(左下)×(底辺全体)(底辺右) ×(右下)(右上) =1

※本ページでは(左上)から反時計回りで記載したが、一周の順番になっていればどこから始めても時計回りでも分子と分母が逆でもいい。
また、メネラウスの定理はチェバの定理と非常によく似ているのですが、チェバの定理は三角形の頂点から引いた3つの直線が一点で交わるときにおける長さの比を求めるのに使用されます。

隣り合わせに置くと､未知の角が等しくなるためが正解です

合同であるといえる条件は以下の3つです。

• ・3辺がそれぞれ等しい
• ・2辺とその間の角がそれぞれ等しい
• ・1辺とその両端の角がそれぞれ等しい

3辺がそれぞれ等しい三角形を2つ用意して、一つの辺を重ねて鏡のように反対側に置きます。
すると、二等辺三角形が2つできることから、角が等しくなることが分かるため、用意した3辺がそれぞれ等しい2つの三角形の角度は3つとも等しいことが分かります。

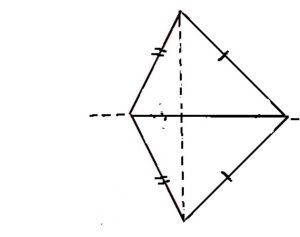
また、合同条件は3つありますが、図形の問題で「長さが等しい」ことを作る問題よりも、「角度が等しい」ことを示す問題の方が作りやすいので、「3辺がそれぞれ等しい」の合同条件を使用することはほとんどありません。

余った辺の引き方は1パターンのためが正解です

合同であるといえる条件は以下の3つです。

• ・3辺がそれぞれ等しい
• ・2辺とその間の角がそれぞれ等しい
• ・1辺とその両端の角がそれぞれ等しい

なお、2辺とその間の角がそれぞれ等しいを満たせば合同であるといえる理屈の概要は以下の通りです。
2辺と3つの頂点は重ねることができ、かつ頂点から別の頂点からの辺の引き方は1パターンしかないことから合同といえます。

残りの頂点の取り方が決まるためが正解です

合同であるといえる条件は以下の3つです。

• ・3辺がそれぞれ等しい
• ・2辺とその間の角がそれぞれ等しい
• ・1辺とその両端の角がそれぞれ等しい

なお、1辺とその両端の角がそれぞれ等しいを満たせば 合同であるといえる理屈の概要を述べると以下の通りです。
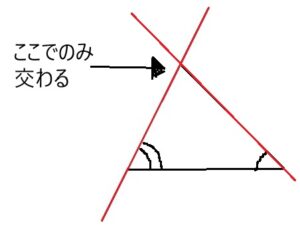
1辺とその両端の角が決められている場合、残りの2つの辺の向きは決められているといえます。
そして、向きの決まっている2つの直線はどこまで延長しようとも、1つの点でしか交わることが無いため､三角形は1パターンしか作れないので、合同であると示せます。

三角形が正解です

「接弦定理」という名前自体は中学校では取り扱いませんが、高校入試などの問題で出てくることもあるので、知っていると役に立つ問題です。以下のように円の中に三角形があるときに、頂点を通る接線が作る角はそれぞれ三角形の残り二つの角の大きさに等しい定理です。

外角と等しいが正解です

円の内接四角形の定理は中学では名前はでてきませんが、たまに証明問題で見えると楽になる場面があります。