一問一答の一歩

直径と円周が正解です

円周は直径と円周の長さの比を表したものであり、具体的な値は以下のようになっています。

• π≒3.14159265358979323……

より具体的な例を挙げて説明すると、直径の円周の関係は以下のようになっています。

• 直径100mmのとき、円の一周の長さは訳314mm直径200mmのとき、円の一周の長さは2倍になって628mmになります。

また、誤答として扱った「半径と円周の関係を利用して考える」方が分かりやすいという考え方もあるので、リンクを共有しておきます。

円が正解です

ざっくりいうと丸い形のことを円といいます。
円は中心となる点からの距離が等しい点の集まりということもできるので、コンパス一つで書くことができます。
また、余談ですが試験会場にコンパスを持っていけない……ということが多々あるので、コンパスがなくてもフリーハンドで円をそれっぽくかける練習しておくと、試験中にときどき役にたったりします。

中心が正解です

中心はその名のとおり、円の真ん中にある点であり、円に関する問題では必ずと言っていいほどよく使用されます。
中心に関する性質としては、中心から円周上にぶつかるように引いた直線(又は線分)の長さは半径の長さと必ず同じになるということは知っておきましょう。
また、他の選択肢については以下の通りです。

• ・焦点……楕円の場合に中心と似た性質を持つ点のペア
• ・中点……一つの線分(直線)の長さを半分に区切る点

半径が正解です

円の中心から端っこまでの長さは半径と呼ばれており、それをさらに2倍の長さにしたものが直径と呼ばれます。
算数や数学では、同じ円上の半径の長さはどれも等しくなることを用いて二等辺三角形を見つけるという流れで使われることが多く、大切なので、半径は覚えておきましょう。

円周が正解です

円の周りの部分を通るので、そのまま円周と呼ばれています。 また、円周に関係する用語としては、以下のものもあるので、合わせて知っておくといいでしょう。

• ・弧……円周のうち指定した2点によって分けられた一部分のこと
• ・弦……弦の両端を結んだ円の内部を通る線分(直線)

弧が正解です

弧と弦の違いは以下の通りです。

• 弧……円周上に沿って結んだ曲線
• 弦……円の内部を通る線分

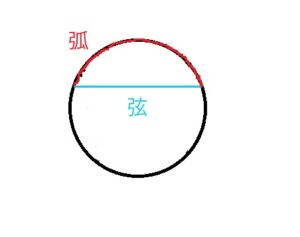
今回は弧を出しましたが、図形の問題では直線の方が扱いやすいため、弦の方が使用される機会が多いです。

扇形が正解です

円の半径を2つ作成し、それに沿って円を切り取ると、扇を広げたような形になるので、おうぎ形と呼ばれます。
おうぎ形は円の一部分であることから、円周、面積は円の円周、面積との比をそれぞれとればいいです。

• 円周:2×π×(半径)×(中心角)/360
• 面積:π×(半径)²×(中心角)/360

πr²が正解です

円でよく問題に出るものとしては大きく分けて以下の2つです。

• ・円周の長さ:πr²
• ・円の面積:πr²

問題では、どちらかというと、円の面積を聞かれることが多いのですが、(円柱や円錐などの)円に関する図形の性質の証明には円周の長さもよく使用されます。

円周を底辺､半径を高さとする三角形が正解です

考え方としては、円にたくさんの半径を引きまます。
この時、円周上の近接する2つの半径と円周の交点を点A,Bとおきます。

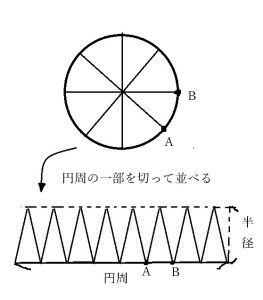
このとき、点A,Bと円の中心2つの半径のなす角度が小さい場合には、以下のような近似が成り立ちます。(誤差の範囲に収めても問題ないといえます。)

• ・底辺……弧ABの長さ
• ・高さ……半径

円をたくさんの三角形に分割したということは。底辺と高さが同じように近似した三角形がたくさんあるといえます。
これらの三角形のの面積を全て足すと、計算の規則により、底辺と高さが以下のような三角形と同じになるといえます。
(変形の長さを仮にr,円周率の大きさを仮にπと表しています。)

• ・底辺……円周の長さ=2πr
• ・高さ……半径=r

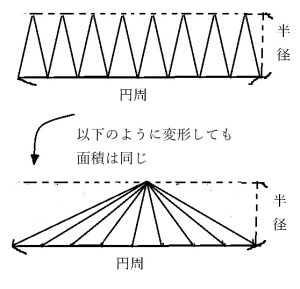
したがって、三角形の面積は(底辺)×(高さ)/2となることから、円の面積は以下の式に近似できます。

• 2πr×r/2=πr²

垂直になるが正解です

証明が感覚的でないため、知らないと見落としやすいのですが、円の接線は接点において半径と必ず垂直になるという特徴があります。問題にも時々出てくることなので、確実におさえておきましょう。

常に等しいが正解です

円周角は知らないと中々出にくい性質であるので、適用出来る図とまとめて覚えておくといいでしょう。

円内部の等しい角度が正解です

円周角については円があったときに等しい角度を求めるのに利用される定理であり、これは言葉よりも以下の図で理解した方が手っ取り早いです。

また、円周角の定理の証明については、補助線として半径を引いて作成した二等辺三角形を用いて行います。

2倍が正解です

中心角の大きさは円周角の大きさの必ず2倍になります。
このことは覚えておけば良いようにも思えますが、もし証明するなら以下のように流れで考えると証明できます。

1. 円の中心から円周角に向けた直線を引く
2. 中心角は1のプロセスで作成された2つの三角形の外角の和であることを確認する。
4. 2で注目した三角形は半径の等しい二等辺三角形であることを確認する。
5. 2つの2等辺三角形の外角の和は円周角の2倍となることを確かめる。