問題1
まっすぐな線のうち、始点と終点が決められているものはどれか
線分が正解です
まっすぐの線は厳密には3種類あり、具体的には以下のような違いがあります。
- 線分……開始の点と終わりの点の両方が決まっている。
- 半直線……開始の点と終わりの点のうちの片方が決まっている。
- 直線……長さや位置の制限のないまっすぐの線
問題2
元の直線に対して垂直な直線
垂線が正解です
垂直とは角度が90°のことをさし、なす角が垂直である直線のことをそのまま垂線と呼びます。
また、他の選択肢に関しては以下の通りです。
- 中線……中点を通る直線
- 二等分線……角度を半分にするように分割する直線
問題3
一つの角の大きさをちょうど半分に区切る線
二等分線が正解です
二等分線は角度を半分にするように分割する直線です。
また、他の選択肢に関しては以下の通りです。
- 中線……中点を通る直線
- 垂直線……元の直線とのなす角が90°である直線
問題4
点と点のちょうど中間点にある点
中点が正解です
点と点のちょうど真ん中にある点であるので中点と呼ばれます。
問題文中で使用する場合は中点であることがサラッとかかれていて、そこから下記の状況であることを用いて問題を解く時のヒントにしていくので合わせておさえておきましょう。
- (中点の左側)=(中点の右側)
問題5
折り曲げてピッタリ重ねることが出来る図形
線対称が正解です
図形の問題においても、二等辺三角形は線対称な図形であるので、片側のことが分かれば自動的にもう片方の性質も分かるときもあるので、知っておくと楽になることもあります。
問題6
180°回転させても回転前と同じ図形になる図形
点対称が正解です
一つの平面上で線を中心に回転させることは出来ないので点対称であることが分かるはずです。
また、平面図形で点対称はあまり出ては来ないのですが、関数(グラフ)の分野で奇関数と呼ばれるものが点対称であることをたまに利用すること
があります。
問題7
対象の中心が存在しているのはどちらか?
点対称が正解です
対象の中心は点のことを指しています。そのため、線対称ではなく、点対称に使われるものであると予想できるはずです。
問題8
対象の軸が存在しているのはどちらか?
線対称が正解です
軸は基本的に直線です。
直線を用いて対称であることを見ているのは線対象だけです。
問題9
2組の対辺が平行である四角形はどれか?
平行四辺形が正解です
四つの辺が必ずいずれかの他の辺と等しくなるので、平行四辺形と呼ばれています。
また、平行四辺形には下記の4つの性質があるので、余裕があれば合わせて知っておくといいでしょう。
- 2組の対辺が平行である
- 2組の対辺の長さが等しい
- 2組の対角の大きさが等しい
- 2組の対角線の交点は必ず各対角線の中点となす
問題10
全ての辺の長さが等しい四角形はどれか?
ひし形が正解です
ひし形のひしは菱(ひし)と呼ばれる植物の葉っぱに似ていることからとられています。 ひし形の特徴は以下の3つです。
- 全ての辺の長さが等しい(定義)
- 2つの対角線は必ず垂直に交わる
- 面積:(対角線)×(対角線)/2
問題11
全て長さが同じ直線によって囲まれた平面図形のことを何というか
正多角形が正解です
正多面体は空間図形の概念です。
また、受験には役に立ちませんが、辺の数Nが整数でない場合も実は存在はしているので、興味があれば見てみるといいでしょう。
問題12
直角三角形の直角と反対側の辺
斜辺が正解です
直角三角形の直角の部分を下においてあげると、水平方向と垂直方向に一辺がそれぞれ出来上がります。
このとき、直角の反対側にある辺の方向は斜め向きであるかのように見えるので
斜辺と呼ばれています。
問題13
ゆがみがない平面上の三角形の内角の和
180°が正解です
歪みのない平面を扱うユークリッド幾何では、平行線の同位角は必ず等しくなります。
そのため、三角形の一つの辺を反対側の角を作っている点を通るように平行移動させると、3つの角の合計が180°になっていることが分かると思います。
問題14
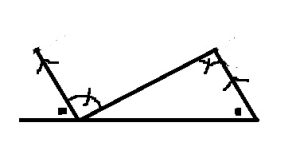
ゆがみがない平面上の四角形の内角の和
360°が正解です
四角形は対角線を引くことによって2つの三角形に分けることができます。
歪みのない空間において、三角形の内角の和は必ず180°になるので、四角形の内閣の和は180を2倍して360°になることが分かります。
余談として、2π[rad]という角度の表し方は弧度法と呼ばれる角度の表し方でよく見る表記であり、通常の角度(度数法)の360°に対応しているのですが、2π°ではなく2π[rad]が正しく、単位が異なっているので誤りです。
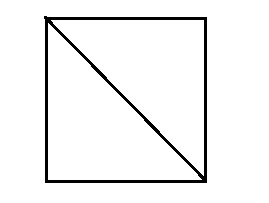
問題15
3角形,4角形,5角形と多角形の数字が1増えると多角形の内角の大きさの合計は何度増えるのか
180°が正解です
多角形の一点からは隣合う頂点以外のところに対角線を引くことができます。
そのため、多角形の数字が1だけ増えると、対角線によって分割することで作成できる三角形の数が1だけ増えるので180°だけ増加します。
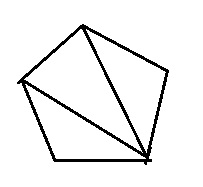
問題16
多角形の角が1増えると内角の和は180°増える。これはどのようにすれば分かる?
一つの角から他の角に対角線を引くが正解です
ちなみに内角、外角の和から外角を引くのは外角の和が360°になることの証明、 全ての辺を一つの頂点に平行移動は三角形の内角の和が180°になることの証明です。
問題17
向かい合った2つの頂点を結んだ直線
対角線が正解です
向かい合う頂点は反対側の角であるともいえるので、対角線と呼ばれています。
対角線については以下のことを知っておくといいでしょう。
- 〇四角形の対角線の性質について
- 対角線の交点は各対角線の中点となる図形……平行四辺形
- 対角線が垂直に交わる図形……ひし形
- 〇対角線の本数の考え方
- ・n角形の対角線の本数……n(n-3)/2
問題18
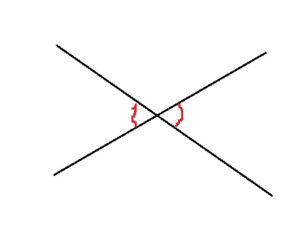
直線同士を結んでできた角と反対側の角
対頂角が正解です
常に反対側にある角であることから対頂角と呼ばれており、対頂角の関係にある角度は常に等しくなる性質があります。
等しくなる理屈としては(隣の角度)との角の大きさの和が必ず180°になることを用いればよく、具体的に式で表すと以下の通りです。
- (もとの角)+(隣の角)=180°……(1)
- (対頂角)+(隣の角)=180°……(2)
- (もとの角)-(対頂角)=0
- (もとの角)=(対頂角)
問題19
以下のうち、高校まで扱う一般的な平面図形の公準として正しいとされるものはどれか
平行線の同位角は等しいが正解です
高校まで扱う平面図形は「ユーグリッド幾何」とも呼ばれています。(これは覚えなくていいです。)
ユーグリッド幾何は平行線公理により「2つの平行線の同位角は等しい」が成り立つ状況を仮定しており、他の性質から導出することはできないのでそのまま覚えましょう。
※厳密には第5公準や平行線公理の対偶であるが、名前は中高の数学のテストにでないので説明の便宜上同じものとする
錯角、同位角が等しくなるのは平行線の場合のみなので、勘違いしないようにしましょう。
問題20
三角形の各辺の垂直二等分線が交わる点
外心が正解です
外心は外接円の中心であり、外接円があるときに使用しうる性質は以下の通りです。
- ・正弦定理
- ・円周角の定理
- ・接弦定理
- ・内接四角形の定理
問題21
三角形の各頂点から対辺の中点を結んだ点
重心が正解です
重心とは、数学よりは物理で大事になってくる概念であり、重心の1点のみを支えてあげれば、倒れずに支えられる点のことをいいます。
また、三角形の重心の数学的な性質を挙げると以下の通りです。
- ・重心は各中線(頂点から対辺の中点を結んだ直線)を2:1に分割する。
問題22
内接円がある時の三角形の面積の導出の考え方
円の接線は半径と垂直が正解です
内接円が与えられている三角形の面積は以下の手順で求めることができます。
- 内接円の中心から頂点に補助線を引く
- 円の接線を底辺、半径を高さとして3つの三角形の面積を計算する。
問題23
三平方の定理は何を求めるための定理か
直角三角形の辺の比を求めるが正解です
三平方の定理は直角三角形の長さの比を求めるための式であり、以下のような形で表されます。
- (斜辺)2=(底辺)2+(高さ)2
また、高校入試や大学入試には一切でないのですが、三平方の定理をさらに発展させたものがフェルマーの最終定理と呼ばれています。
問題24
図形の広さのこと
面積が正解です
面の大きさを2つのかけ算の答えである積で表していることから面積と言われます。
また、面積の基準は縦が1cm,横が1cmの正方形状のタイルを何枚敷き詰めることができるかを用いて考えられ、単位はcm2がよく使用されます。
問題25
1m2の読み方
平方メ一トルが正解です
広さを示す面積の基準は1辺が1cmの正方形が使用されており、方は「四角形の」という意味を持ちます。
また、平面における広さを表しているので、平という字が使用されて平方とされています。
なお、右上にある添え字の2は同じものを2回かけているという意味があり、単位がcmであるものを2回かけていることからcm2とされています。
- cm×cm=cm2
問題26
正方形の面積
1辺×1辺が正解です
正方形の面積も長方形と同じように、1辺が1cmのタイルが何枚入るかを用いて考えます。
ただし、正方形の場合は1つの辺が分かってしまえば、縦の長さも横の長さも同じであることが分かっているので、1辺×1辺で問題ないといえます。
問題27
長方形の面積
縦×横が正解です
面積は1cmの正方形のタイルを何枚敷き詰められるかで考えます。
長方形の場合は横に敷き詰めてある正方形のタイルの数はどの行を見ても必ず等しくなります。
そのため、いちいちどの行に何列あるかを数えなくとも、1列分のタイルの数が分かっていればかけ算で求められます。
縦のタイルの数と横のタイルの数はそれぞれ縦の長さ、横の長さに該当するので解答の通りとなります。
問題28
平行四辺形の面積公式
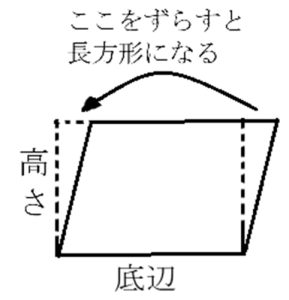
底辺×高さが正解です
平行四辺形の高さとなる直線にそって平行四辺形を2つに切って、左にずらすと、辺を必ず重ねることができます。
辺を重ねた後は縦が高さに該当し、底辺の長さが横に該当するので面積公式は解答の通りになります。
問題29
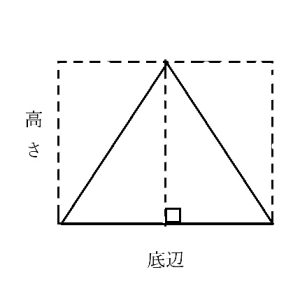
三角形の面積公式
底辺×高さ/2が正解です
三角形の高さを示す直線で三角形を2つに区切ると、2つの直角三角形が現れます。
そして、各直角三角形は長方形を半分にしたものであることが感覚的に分かると思います。
そのため、全体の三角形の面積も長方形の面積の(底辺)×(高さ)の半分になることが分かるはずです。