一問一答の一歩

直方体が正解です

全ての角が直角で、なおかつ方は四角という意味を表していることから、直方体と呼ばれています。
また、形は箱状のものと考えるとイメージしやすいです。

角柱が正解です

空間図形のうち、代表的な直方体や立方体も角柱の一部の四角柱の一部です。
角柱では、底面が長方形ではない図形(三角形など)を取り扱います。
形は多少変わりますが、基本的な考え方は直方体とはそんなに変わらないです。

円柱が正解です

円状の柱でありことからそのまま円柱と呼ばれており、形は下記の通りです。

なお、他の選択肢についても説明すると以下の通りです。

• ・円環体……ドーナッツ型(高校までの数学では出ない)
• ・円錐……底面は円であるが、上端はとんがっている図形

球が正解です

球は数学的には扱いが難しいので、あまり問題として出題はされにくいです。
中学の内容ですが、球の数学的な性質をあげておくと以下の通りです。

• ・表面積=4×円周率×半径²
• ・体積=43×円周率×半径³

面が正解です

面と辺はそれぞれ図形の境界になっているという点では同じなのですが、以下の違いがあります。

• ・面……図形の境界となる平面
• ・辺……図形の境界となる線

5種類が正解です

正多面体の種類は以下の5つのみとされています。

• ・正四面体
• ・正六面体(立方体)
• ・正八面体
• ・正十二面体
• ・正二十面体

これは知っていないと「無限に存在する」と勘違いしやすいので、知識として覚えておきましょう。
理屈はとしては難しめの「オイラーの多面体定理」を用いて解説されるのですが、気が向いたら見てみるといいでしょう。

ねじれの位置が正解です

本来同一平面上にあれば向きの違っている2直線は交わっているにも関わらず、交わらない様子がねじれているように見えることからねじれの位置と呼ばれています。
また、他の選択肢については以下の通りです。

• ・垂直……2直線のなす角が90°
• ・平行……向きが同じであるが故に交わることの無い2直線の関係

底面が正解です

立体を考えるときには、平行になっている2つの面を上下にすると分かりやすいです。
(問題集にも書かれている見取り図は大抵平行な面を上下に設定されています。)
そのため、原則立体の底に当たる面であるので、底面と呼ばれています。

側面が正解です

数学の問題で出てくる立体は二つの平行な面を上下に記載することが一般的とされています。
そのため、上下の面とされ以外の面では取り扱いを分けることが多いので、上下の面でない面のことを側面と呼びます。

展開図が正解です

空間図形に関する図については以下の通りです。

• ・立面図……真横から見た図
• ・平面図……真上から見た図
• ・投影図……立面図と平面図を組み合わせて立体を表現する書き方
• ・展開図……辺に沿って切ったときの図
• ・断面図……立体をぶった斬った時の断面となる図
• ・見取図……立体の全体の形が分かるように描いた図

下記のように辺に沿って切り開いて、平面の上に描いた図が箱を開けた形のように見えることから展開図と呼ばれています。

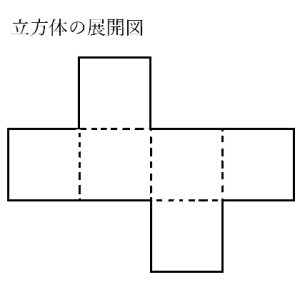
展開図はたまに使われるイメージですが、具体的には以下の状況で使用されます。

• 面上に沿って移動する場合の最短距離を求める場合

立面図が正解です

空間図形に関する図については以下の通りです。

• 立面図……真横から見た図
• 平面図……真上から見た図
• 投影図……立面図と平面図を組み合わせて立体を表現する書き方
• 展開図……辺に沿って切ったときの図
• 断面図……立体をぶった斬った時の断面となる図
• 見取図……立体の全体の形が分かるように描いた図

母線が正解です

円錐の展開図を描いた時に、側面はおうぎ形になるので、側面のおうぎ形の中心角や円錐の表面積を求めたりするのによく利用されます。

体積が正解です

立体の大きさをかけ算を用いた積を用いて表すことから体積と呼ばれています、
また、体積の基準は一辺が1cmのサイコロが基準となっています。 また、単位の右上にある小さな3の添え字は同じものをかけているということを示しており、イメージとして表すと、以下の通りです。

• cm×cm×cm=cm³

1立方センチメ一トルが正解です

漢字の一つである「立」の字に関しては縦と横だけでなく、高さまで考慮しているので、図形が立ちあがっている状態のように見えることから使われています。
また、方については、「四角形の」という意味があり、体積の基準は1辺が1cmのサイコロということから使用されています。
これらのことから、「1立方センチメ一トル」と呼び方をされています。
また、上についている添え字の3は同じものを3回かけているという「累乗」の意味をもっており、縦の単位がcm、横の単位がcm、高さの単位がcmであり、単位がcmのものを3回かけていることからcm³という表記をされています。

縦×横×高さが正解です

体積は「全ての辺の長さが1c,mのサイコロ何個分の大きさか」という観点から考えていきます。
そのため、面積に加えて、高さの文もかけてあげればいいので、直方体の体積は以下のようになります。

• 体積=底面積×高さ=縦×横×高さ

3倍が正解です

底面積と高さが等しい四角柱と四角錐の体積を比較すると、以下の関係があります。

• (四角柱の体積)=3×(四角錐の体積)

これは、補助線を引いて求めることができ、概要を述べると以下の通りです。

1. 1辺の長さが1の立方体を考える。
2. 反対側の頂点への対角線を4組引く。
3. 対角線を用いて6つの四角錐を考える。
4. 対象の四角錐は高さが12であり、体積は16であることを確認する。

立方体の反対側の頂点を引くが正解です

なお、各高さごとの面積を力技で出すことは積分の考え方になるので、本問題(中学生に説明する場合)では不適切です。
錘体の体積は13と覚えてもいいのです。
しかし、なぜそうなるのかも合わせていつでも作れるようにしておくと、ど忘れしたときにすぐに思い出しやすくなります。
(無意味な暗記より、意味の分かるもののほうが、人は記憶に強く残りやすいため)

√3倍が正解です

このことが聞かれることはほとんどないのですが、知っていると大幅に計算時間を短縮できる上に、割と覚えやすい形であるが故に出題しました。
計算の理屈は以下の通りです。 一つの面の正方形の辺の長さをdとすると、三平方の定理より正方形の斜辺の長さはいかのようになります。

• √d²+d²=d√2

そして、求める立方体の反対側の頂点までの長さは、立方体の1辺、正方形の対角線をそれぞれ底辺､高さとする直角三角形の斜辺の長さに等しくなります。
そのため、三平方の定理より、求める長さは以下のようになります。

• d√1+2=d√3