問題1
半径がrの円の面積公式(ただし、円周率はπと表している)
πr2が正解です
円でよく問題に出るものとしては大きく分けて以下の2つです。
- ・円周の長さ:πr2
- ・円の面積:πr2
問題2
三角比(sinθ)を使わずに円の面積公式を導出する考え方はどれか?
円周を底辺、半径を高さとする三角形が正解です
考え方としては、円にたくさんの半径を引きまます。
この時、円周上の近接する2つの半径と円周の交点を点A,Bとおきます。
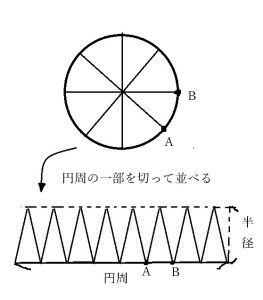
このとき、点A,Bと円の中心2つの半径のなす角度が小さい場合には、以下のような近似が成り立ちます。(誤差の範囲に収めても問題ないといえます。)
- ・底辺……弧ABの長さ
- ・高さ……半径
これらの三角形のの面積を全て足すと、計算の規則により、底辺と高さが以下のような三角形と同じになるといえます。
(変形の長さを仮にr,円周率の大きさを仮にπと表しています。)
- ・底辺……円周の長さ=2πr
- ・高さ……半径=r
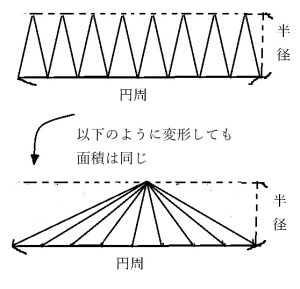
したがって、三角形の面積は(底辺)×(高さ)/2となることから、円の面積は以下の式に近似できます。
- 2πr×r/2=πr2
問題3
円の接線と半径の関係
垂直になるが正解です
証明が感覚的でないため、知らないと見落としやすいのですが、円の接線は接点において半径と必ず垂直になるという特徴があります。問題にも時々出てくることなので、確実におさえておきましょう。
問題4
円周角の定理は何を求めるために使用されるか
円内部の等しい角度が正解です
円周角については円があったときに等しい角度を求めるのに利用される定理であり、これは言葉よりも以下の図で理解した方が手っ取り早いです。

また、円周角の定理の証明については、補助線として半径を引いて作成した二等辺三角形を用いて行います。
問題5
接弦定理は円の中にどの図形があるときに使用することができるか
三角形が正解です
「接弦定理」という名前自体は中学校では取り扱いませんが、高校入試などの問題で出てくることもあるので、知っていると役に立つ問題です。以下のように円の中に三角形があるときに、頂点を通る接線が作る角はそれぞれ三角形の残り二つの角の大きさに等しい定理です。

問題6
円に内接する四角形において、一つの角の大きさはむかいあう角の大きさとはどのような関係があるか
外角と等しいが正解です
円の内接四角形の定理は中学では名前はでてきませんが、たまに証明問題で見えると楽になる場面があります。
