問題1
確率と統計学を結ぶ、試行回数が大きいときの相対度数は確率に近似できる現象
大数の法則が正解です
大数の法則は統計と確率を結ぶ非常に有効な概念であり。1000回以上の大量のサンプルがある場合の相対度数は確率に近似することができます。
統計と確率が結びついていることで、少数のサンプルでも確率から未来をある程度予想することができたり、確率に関して平均や標準偏差のような統計情報をえることもできます。
問題2
選んで並べる場合、樹形図の分岐パターンはどのように変化していくか
1ずつ減るが正解です
樹形図の分岐のパターンは以下の2つに別れています
- ・規則的な樹形図
- ・不規則の樹形図
- ・分岐パターンが1ずつ減るパターン
- ・分岐パターンが不変のパターン
上記の樹形図の分岐のパターンを書き出してみると以下のように分岐することが分かるはずです。
- 4パターン
- →3パターン
- →2パターン
- →1パターン
問題3
サイコロを複数回振るような重複を許す並べ替えの場合、樹形図の分岐はどのように変化していくか?
常に不変が正解です
樹形図の分岐のパターンは以下の2つに別れています
- ・規則的な樹形図
- ・不規則の樹形図
- ・分岐パターンが1ずつ減るパターン
- ・分岐パターンが不変のパターン
問題4
選ぶだけ(順不同)の場合の数は選んで並べる(順番関係あり)場合の数にどんな補正を加えれば求められるか
並べ替えパターンで割るが正解です
樹形図をそのまま書こうとすると、選ぶだけ(順番関係なし)は分岐パターンが不規則系であり、抜けや漏れが起こりやすいので、規則系である「選んで並べる」に補正を加えると考えるとやりやすいです。
具体的な補正の考え方はこの場で説明するとどうしても長くなってしまうため、本文中のリンク先を参考にするといいでしょう。
問題5
n個のものを並べ替えるときに用いる式はどれか
n!が正解です
n個のものを並べ替えるときに用いる式は階乗と呼ばれており、以下のように表されます。
- =n!
- =n×(n-1)×……×2×1
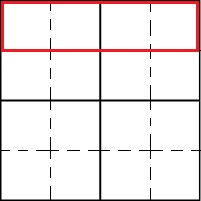
余談ですが、数字の並べ替えを用いたパズルとしてメジャーなものとしては、各行、各列で同じ数字が被らないように数字を並べる数独というものがあり、それの1行目赤枠部分を作ると考えると比較的イメージつきやすいと思います。
※なお、2列目以降については少し面倒になるので気になる方下記リンクを参考にしてみてください。
また、覚える必要は全くありませんが、もう一つの選択肢のΓ(n)は階乗を一般化したものはガンマ関数と呼ばれています。(中に入る変数が誤っているので不正解となっています)
問題6
選んで順番に並べる場合の数を求めるのにしようするものはどちらか
nPrが正解です
場合の数の表記の仕方と対応は以下の通りです。
- ・並べ替えるだけ……n!=n×(n-1)×……×2×1
- ・選んで並べる……nPr=n×(n-1)×……(n-r)
- ・選ぶだけ(順不動)……nCr=nPr/r!
問題7
選ぶだけ(順不同)の場合の数を求めるのに使用するものはどちらか
nCrが正解です
場合の数の表記の仕方と対応は以下の通りです。
- ・並べ替えるだけ……n!=n×(n-1)×……×2×1
- ・選んで並べる……nPr=n×(n-1)×……(n-r)
- ・選ぶだけ(順不動)……nCr=nPr/r!
問題8
円順列の考え方
一つを固定するが正解です
円順列は以下のように最後→最初の順番が成立する場合も同じと扱うと以下のものが全て同じと扱われます。
例、1~4の数字を円状に並べる円順列では以下のものが全て同じものとして扱われます。
- 1、2、3、4
- 2、3、4、1
- 3、4、1、2
- 4、1、2、3
- (n-1)!
問題9
図形の辺と対角線の合計を求める問題
組み合わせの問題が正解です
図形の辺と対角線の合計はあらかじめn個の頂点が用意されている状況で頂点の中から2つを選んで結ぶと考えると分かりやすいです。
すると、選ぶ順番に関しては順不同であるので、求める辺と対角線の合計は以下の通りになります。
- nC2
問題10
対角線を用いて三角形を作る問題
組み合わせの問題が正解です
図形の辺と対角線の合計はあらかじめn個の頂点が用意されている状況で頂点の中から2つを選んで結ぶと考えると分かりやすいです。
すると、選ぶ順番に関しては順不同であるので、求めるものは以下の通りになります。
- nC2
問題11
文字列の並べ方のパターン(例SUUGAKU)は何の問題と考えるべきか
同じものを含む順列が正解です
仮に3つあるUをU1、U2、U3区別できるようにしたとすると、以下の6つは同じものとして扱われます。
- SU1U2GAKU3
- SU1U3GAKU2
- SU2U1GAKU3
- SU2U3GAKU1
- SU3U1GAKU2
- SU3U2GAKU1
- 7!3!
問題12
最短距離の道のパターンの数の場合の数はどんな考え方をするか?
同じものを含む順列が正解です
最短距離の道のパターンの数は矢印の並べ替えと考えます。
その際、同じ向きの矢印に関しては順不同であるので、同じものを含む順列と考えます。
問題13
同時に起こることのない二つの現象の関係性のことを何というか
排反が正解です
排反の例を挙げると、一つのくじを引いた時にそれが当たりくじであり、かつ同時にハズレくじでもある状況にはなり得ないということが挙げられます。
また、排反に関するパラドックスにも興味深いものがあるので、興味のある人は観てみると面白いでしょう。
問題14
○○の出来事に対してその出来事が起こらない確率のことは何と呼ばれているか
余事象が正解です
ある物事Pが起こらない確率はPの余事象と呼ばれており以下のような関係式が成り立ちます。
- (Pの余事象の確率)=1-(Pがおこる確率)
例としてはガチャを何回も引いて少なくとも1回は当たる確率などが余事象の考え方を用いて計算されます。
問題15
1回目の事象の確率が以降の事象の確率に影響を与えないこと
独立が正解です
また、独立ではない状況のことは反対に従属と呼びます。
確率における独立と従属もややこしいので具体例をあげると以下のようになります。
〇従属している例
箱の中に3つのひもがあり、当たりのひもが一つ入っている場合に二人目が当たりのひもを引く確率は一人目の結果に左右される。(くじは戻さないものと仮定している)
- 1人目が当たる確率……13
- 2人目が当たる確率……(一人目が当たったら0,一人目が外れたら12)
コインを複数回投げる場合、以下の二つの確率は等しくなります。
- 1回目に裏が出る確率
- 2回目に裏が出る確率
問題16
確率変数の平均。つまり、ギャンブルをした時に得られる金額の指標となるものはどれか
期待値が正解です
期待値、分散、標準偏差は確率統計においては重要な数字であり、確率変数(上の例だと貰えるお金)をXとした時に以下のように表されます
- ・期待値……E(X)
- ・分散……V(X)
- ・標準偏差……S(X)
標準偏差は起こりうる値、つまりギャンブルでいう貰えるお金のばらつきの大きさを示した値です。ギャンブルで標準偏差が大きい場合は以下のように期待値の使用が不適切になる場合もあります。
また、他の選択肢である最頻値は統計の分野の用語で、一番数の多いデータの値のことを指します。
問題17
確率において、期待値は一般的にどのように表されるか
E[X]が正解です
期待値はexpectedvalueの頭文字をとってE[X]と表されます。
ここで使用されているXは確率変数と呼ばれており、対応する確率が発生したときの結果のことを示しています。
例を挙げると、当たったらお金をもらえるくじを考えると、当たる確率とは別に存在する当たったときにもらえる金額が確率変数Xに当てはまります。
問題18
それぞれのパターンの起こる確率のばらつき具合を示したものはどれか
標準偏差が正解です
標準偏差はたくさんあるデ-タの散らばり具合を示す指標の一つであり、ざっくりと言うとデ-タが平均値からどのくらい離れているか平均をとったようなイメージです。
(厳密には少し違ってはいますが……)
平均値が同じでも、散らばり具合いによってデ-タの傾向は変わるので大事な指標の一つです。
問題19
標準偏差の表し方
σ[X]が正解です
確率統計の代表値は以下のように表されます。
- 期待値……E[X]
- 分散……V[X]
- 標準偏差……σ[X]
問題20
起こる確率pのものがn回起こる反復施行の確率の式として適切なものはどれか?
nCrpr(1-p)1-rが正解です
起こる確率pのものがn回起こる事象の一つは以下の式で表されます。
- pr(1-p)1-r
問題21
離散的な反復施行の確率分布のことは何と呼ばれるか
二項分布が正解です
離散的な反復施行の確率分布は二項分布と呼ばれる特殊な確率分布であり、1回ごとの確率をp、試行回数をnとすると期待値E[X]と分散V[X]は以下のようになります。
- E[X]=np
- V[X]=np(1-p)
また、連続的な確率変数Xにおいて、二項分布をとると正規分布に近似することができます。
問題22
3つのドアの中に当たりの扉は1つある。このとき、ランダムに選んだ場合、当たる確率はいくらか
1/3が正解です
確率は以下の計算方法によって計算を行います。このことは直観的に理解できると思うので、覚えておきましょう。
- 求めるものが発生するパターン 全パターン
- (求めるものが発生するパターン)……当たりの扉は一つだけであるので1パターン
- (全パターン)……開ける扉が3つあるので3パターン
問題23
ある前提となる条件を満たしていることが分かった状態で、さらに別の追加条件も満たす確率は何というか
条件付き確率が正解です
ある前提となる条件を満たしていることが分かった状態で、さらに別の追加条件も満たす確率に関しては以下のようにかんがえます。
- ・分子→別の追加条件を満たす場合の数
- ・分母→前提となる条件を満たしている場合の数
- 「ジョーカーを抜いた52枚のトランプが山札にある、このカードの山から新たに3枚のカードを抜き取ると、全てダイヤであった。このとき、箱の中のカードがダイヤである確率はいくらか」
問題24
ある家庭に子どもが二人いる。子どものうち一人は男の子であることがわかっているとき、2人とも男の子である確率はいくらか。ただし、男の子、女の子が生まれてくる確率は同じものとする。
13が正解です
これは2人の子ども問題と呼ばれるものであり、こちらも条件付き確率の例の一つです。
具体的な考え方は以下の通りです。
- 2人兄弟の性別のパターンは4通り
- 前提条件を満たすパターンは4通りから両方とも女であるパターンを抜くので3パターン。
- また、両方とも男であるパターンは1パターンのみであるため、13となります。





