問題1
ゆがみがない平面上の三角形の内角の和
180°が正解です
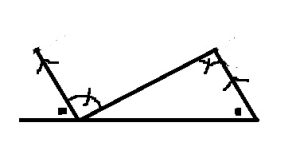
歪みのない平面を扱うユークリッド幾何では、平行線の同位角は必ず等しくなります。
そのため、三角形の一つの辺を反対側の角を作っている点を通るように平行移動させると、3つの角の合計が180°になっていることが分かると思います。
問題2
ゆがみがない平面上の四角形の内角の和
360°が正解です
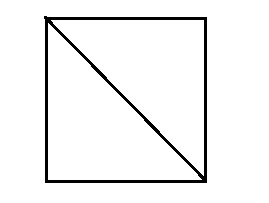
四角形は対角線を引くことによって2つの三角形に分けることができます。
歪みのない空間において、三角形の内角の和は必ず180°になるので、四角形の内閣の和は180を2倍して360°になることが分かります。
余談として、2π[rad]という角度の表し方は弧度法と呼ばれる角度の表し方でよく見る表記であり、通常の角度(度数法)の360°に対応しているのですが、2π°ではなく2π[rad]が正しく、単位が異なっているので誤りです。
問題3
3角形,4角形,5角形と多角形の数字が1増えると多角形の内角の大きさの合計は何度増えるのか
180°が正解です
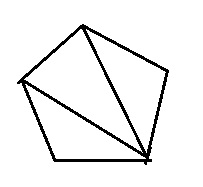
多角形の一点からは隣合う頂点以外のところに対角線を引くことができます。
そのため、多角形の数字が1だけ増えると、対角線によって分割することで作成できる三角形の数が1だけ増えるので180°だけ増加します。
問題4
多角形の角が1増えると内角の和は180°増える。これはどのようにすれば分かる?
一つの角から他の角に対角線を引くが正解です
ちなみに内角、外角の和から外角を引くのは外角の和が360°になることの証明、 全ての辺を一つの頂点に平行移動は三角形の内角の和が180°になることの証明です。
問題5
向かい合った2つの頂点を結んだ直線
対角線が正解です
向かい合う頂点は反対側の角であるともいえるので、対角線と呼ばれています。
対角線については以下のことを知っておくといいでしょう。
- 〇四角形の対角線の性質について
- 対角線の交点は各対角線の中点となる図形……平行四辺形
- 対角線が垂直に交わる図形……ひし形
- 〇対角線の本数の考え方
- ・n角形の対角線の本数……n(n-3)/2
問題6
角度が90°であることの別名は何と呼ばれているか?
直角が正解です
直角はざっくりいうと、横方向の向きと縦方向の向きの違いと考えるとイメージしやすいです。
また、以下のものは全て同じ意味を持つので、頭の中で対応できるようにしておきましょう。
- 直角
- 垂直
- 角度が90°
- 角度がπ/2ラジアン
問題7
図形の広さのこと
面積が正解です
面の大きさを2つのかけ算の答えである積で表していることから面積と言われます。
また、面積の基準は縦が1cm,横が1cmの正方形状のタイルを何枚敷き詰めることができるかを用いて考えられ、単位はcm2がよく使用されます。
問題8
1m2の読み方
平方メ一トルが正解です
広さを示す面積の基準は1辺が1cmの正方形が使用されており、方は「四角形の」という意味を持ちます。
また、平面における広さを表しているので、平という字が使用されて平方とされています。
なお、右上にある添え字の2は同じものを2回かけているという意味があり、単位がcmであるものを2回かけていることからcm2とされています。
- cm×cm=cm2
問題9
正方形の面積
1辺×1辺が正解です
正方形の面積も長方形と同じように、1辺が1cmのタイルが何枚入るかを用いて考えます。
ただし、正方形の場合は1つの辺が分かってしまえば、縦の長さも横の長さも同じであることが分かっているので、1辺×1辺で問題ないといえます。
問題10
長方形の面積
縦×横が正解です
面積は1cmの正方形のタイルを何枚敷き詰められるかで考えます。
長方形の場合は横に敷き詰めてある正方形のタイルの数はどの行を見ても必ず等しくなります。
そのため、いちいちどの行に何列あるかを数えなくとも、1列分のタイルの数が分かっていればかけ算で求められます。
縦のタイルの数と横のタイルの数はそれぞれ縦の長さ、横の長さに該当するので解答の通りとなります。
問題11
平行四辺形の面積公式
底辺×高さが正解です
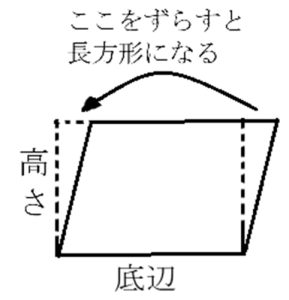
平行四辺形の高さとなる直線にそって平行四辺形を2つに切って、左にずらすと、辺を必ず重ねることができます。
辺を重ねた後は縦が高さに該当し、底辺の長さが横に該当するので面積公式は解答の通りになります。
問題12
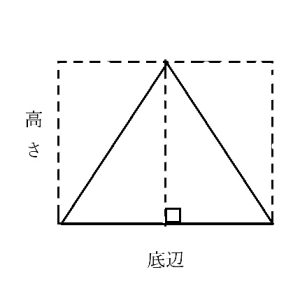
三角形の面積公式
底辺×高さ/2が正解です
三角形の高さを示す直線で三角形を2つに区切ると、2つの直角三角形が現れます。
そして、各直角三角形は長方形を半分にしたものであることが感覚的に分かると思います。
そのため、全体の三角形の面積も長方形の面積の(底辺)×(高さ)の半分になることが分かるはずです。
問題13
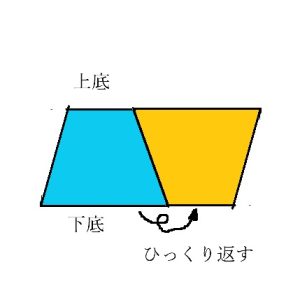
台形の面積公式
(上底+下底)×高さ/2が正解です
台形を上下ひっくり返して横に並べると、必ず平行四辺形になります。
この時の平行四辺形の底辺は(上底+下底)に一致します。
しかし、この時できた平行四辺形の面積は台形2つ分の面積であるため、半分にして開ける必要があることから2で割っています。
問題14
ひし形の面積公式
(対角線×対角線)/2が正解です
ひし形の対角線は必ず直角に交わる性質があります。
そのため、一つの対角線Aを用いてひし形を2
つの三角形に分割した時、必ずもう一つの対角線Bは三角形の高さに該当します。
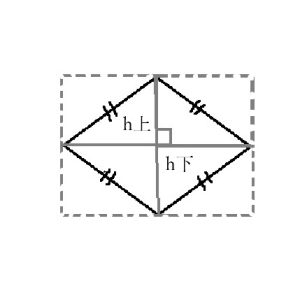
ここで、一つの対角線Aがもう一つの対角線Bの長さをh上とh下に分割した場合、各三角形の面積は(底辺)×(高さ)/2であることから以下のようになります
- 高さがh上の三角形の面積:(対角線A)×h上/2
- 高さがh下の三角形の面積:(対角線A)×h下/2
- (対角線A)×(h上+h下)/2
問題15
半径がrの円の面積公式(ただし、円周率はπと表している)
πr2が正解です
円でよく問題に出るものとしては大きく分けて以下の2つです。
- ・円周の長さ:πr2
- ・円の面積:πr2
問題16
三角比(sinθ)を使わずに円の面積公式を導出する考え方はどれか?
円周を底辺、半径を高さとする三角形が正解です
考え方としては、円にたくさんの半径を引きまます。
この時、円周上の近接する2つの半径と円周の交点を点A,Bとおきます。
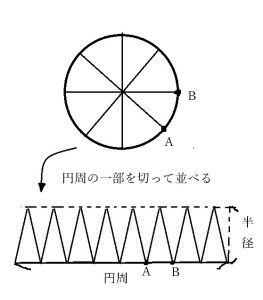
このとき、点A,Bと円の中心2つの半径のなす角度が小さい場合には、以下のような近似が成り立ちます。(誤差の範囲に収めても問題ないといえます。)
- ・底辺……弧ABの長さ
- ・高さ……半径
これらの三角形のの面積を全て足すと、計算の規則により、底辺と高さが以下のような三角形と同じになるといえます。
(変形の長さを仮にr,円周率の大きさを仮にπと表しています。)
- ・底辺……円周の長さ=2πr
- ・高さ……半径=r
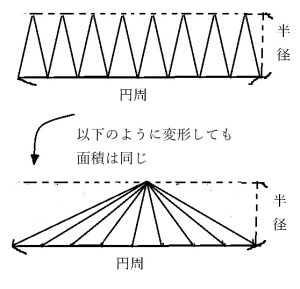
したがって、三角形の面積は(底辺)×(高さ)/2となることから、円の面積は以下の式に近似できます。
- 2πr×r/2=πr2